What Is the Volume of the Prism to the Nearest Whole Unit

Triangular Prism Estimator

Created past Hanna Pamuła , PhD candidate and Jasmine J Mah

Reviewed past

Bogna Szyk and Jack Bowater

Last updated:

Sep 23, 2021

Tabular array of contents:

• Triangular prism - what's that?
• Triangular prism formulas
• Triangular prism volume
• Triangular prism surface area
• How to observe the volume of a triangular prism with this tool?
• FAQ

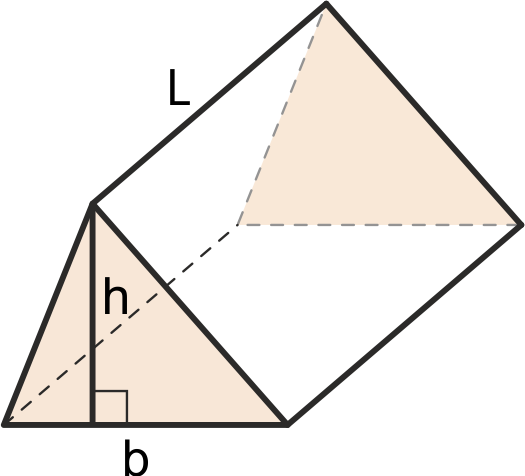
If you ever wondered how to find the volume of a triangular prism, this triangular prism reckoner is the thing you are looking for. Not only can it calculate the volume only also may be helpful if yous need to determine the triangular prism surface area. Choose the option which fits your needs and experiment with the tool! If you are curious about triangular prism formulas behind the calculator, scroll downwards to find out more.

Triangular prism - what's that?

What is a prism? Information technology'southward a solid object with:

• identical ii bases
• 3 rectangular faces (correct prism) or in parallelogram shape (oblique prism)
• the same cross department along its whole length

We are using the term triangular prism to describe the right triangular prism, what is quite a common practice. If yous are looking for other prism type, cheque our rectangular prism calculator.

Triangular prism formulas

Normally what you need to calculate are the triangular prism volume and its area. The ii most basic equations are:

• volume = 0.5 * b * h * length, where b is the length of the base of operations of the triangle, h is the height of the triangle and length is prism length

• area = length * (a + b + c) + (two * base_area), where a, b, c are sides of the triangle and base_area is the triangular base surface area

Merely what if we don't take the height and base of operations of the triangle? And how to find triangular prism surface surface area without all sides of the triangular base of operations? Check out the other triangular prism formulas!

Triangular prism volume

In the triangular prism figurer y'all tin easily discover out the volume of that solid. A general formula is volume = length * base_area; the one parameter you ever need to have given is the prism length, and there are four ways to calculate the base - triangle area. Our triangular prism figurer has all of them implemented, isn't it awesome?

The specific formulas await as follows:

• Length * Triangular base expanse given triangle base and elevation

  It's this well-known formula mentioned earlier:

  volume = length * 0.v * b * h

• Length * Triangular base area given three sides (SSS)

  If you know the lengths of all sides, use the Heron'south formula to find the area of triangular base of operations:

  volume = length * 0.25 * √( (a + b + c) * (-a + b + c) * (a - b + c) * (a + b - c) )

• Length * Triangular base area given ii sides and the angle between them (SAS)

  You lot tin calculate area of a triangle easily from trigonometry:

  book = length * 0.5 * a * b * sin(γ)

• Length * Triangular base area given two angles and a side betwixt them (ASA)

  You can summate that using trigonometry:

  volume = = length * a² * sin(β) * sin(γ) / (2 * sin(β + γ))

Triangular prism surface area

If you lot want to calculate the surface surface area of the solid, the most well-known formula is the 1 given three sides of the triangular base of operations :

• surface area = length * (a + b + c) + (2 * base_area) = length * base_perimeter + (two * base_area)

However, we don't always have the three sides given. What then?

• Triangular base: given 2 sides and the angle between them (SAS)

  Using law of cosines, we tin can find the tertiary triangle side:

  area = length * (a + b + √( b² + a² - (two * b * a * cos(angle)))) + a * b * sin(bending)

• Triangular base: given 2 angles and a side between them (ASA)

  Using law of sines, we can find the two sides of triangular base:

  area = (length * (a + a * (sin(angle1) / sin(angle1+angle2)) + a * (sin(angle2) / sin(angle1+angle2)))) + a * ((a * sin(angle1)) / sin(angle1 + angle2)) * sin(angle2)

The only selection when you can't calculate triangular prism volume is having given triangle base and its height (do y'all know why? Think almost it for a moment). All the other versions may be calculated with our triangular prism computer.

Let'south check what's the volume and surface expanse of a tent shaped like a triangular prism:

1. Find out what's the length of the triangular prism. Assume it's equal to 80 in, type this value into the first box of triangular prism calculator.
2. Choose the selection with your parameters given. For example, given three sides of our base.
3. Enter base sides. Our tent has a = 60 in, b = fifty in and c = l in.
4. Triangular prism surface surface area and volume announced in no time. It's 96,000 cu in (55.56 cu ft) and 15,200 in² (105.56 ft²).

FAQ

What is a triangular prism?

It is a shape that is formed by wrapping 2 parallelly faced triangles as peak and bottom faces. A triangular prism is a polyhedron with a triangle as base and rectangles equally lateral faces.

How to describe a triangular prism?

To draw a triangular prism:

1. Describe the base of the prism as a triangle.
2. Draw the top face of the prism as a triangle parallel to the base.
3. Join the corresponding vertices of both triangles i.e., base and top faces.

How many edges exercise a triangular prism have?

A triangular prism has 9 edges, with three each forming bottom and top faces. The residue of them form the lateral faces.

How many faces do a triangular prism have?

A triangular prism has 5 faces, i.east., a base and top face up forth with the iii lateral faces.

How many vertices exercise a triangular prism have?

A triangular prism has 6 vertices, i.e., 3 each on top and bottom triangular faces.

Hanna Pamuła , PhD candidate and Jasmine J Mah

Area of a hemisphere Cube Cube Calc: find v, a, d … sixteen more

smithwhard1991.blogspot.com

Source: https://www.omnicalculator.com/math/triangular-prism